Simple Interest vs. Compound Interest: Calculation Techniques

Understanding the difference between Simple Interest and Compound Interest is fundamental in finance, as it helps you make informed decisions about investments, loans, and savings. Both involve paying or earning interest, but their calculation methods significantly impact the growth of your investments or the total cost of a loan. In this blog, we’ll explore the calculation techniques for each and illustrate how to use them effectively.

What is Simple Interest?

Simple Interest is a method of calculating interest only on the initial amount, or principal, for the entire duration of an investment or loan. It does not consider the effect of compounding, making it straightforward and predictable.

Formula for Simple Interest:

SI = P × r × t

Where:

• SI = Simple Interest
• P = Principal (Initial investment or loan amount)
• r = Interest rate per period (expressed as a decimal)
• t = Time (in years)

Example:

If you invest ₹1,000 at a 5% interest rate for 3 years, the simple interest calculation would be:

SI = 1000 × 0.05 × 3 = 150

So, the interest earned over 3 years is ₹150, resulting in a total amount of ₹1,150.

What is Compound Interest?

Compound Interest builds upon the idea of simple interest by adding interest to the principal and previously accumulated interest. This means you earn "interest on interest," resulting in exponential growth over time.

Formula for Compound Interest:

A = P × (1 + r/n)^(n × t)

Where:

• A = Amount (Future Value)
• P = Principal (Initial investment or loan amount)
• r = Annual interest rate (as a decimal)
• n = Number of times interest is compounded per year
• t = Time (in years)

Example:

If you invest ₹1,000 at a 5% annual interest rate for 3 years, compounded annually:

A = 1000 × (1 + 0.05/1)^(1 × 3) = 1000 × (1.05)^3 = 1157.63

The total amount is ₹1,157.63, with the interest earned being ₹157.63.

Key Differences Between Simple and Compound Interest

1. Interest Calculation:
   

• Simple Interest: Interest is calculated only on the principal.
  
• Compound Interest: Interest is calculated on both the principal and accumulated interest.
  

2. Growth Pattern:
   

• Simple Interest: Grows linearly; the interest earned remains the same each period.
  
• Compound Interest: Grows exponentially, with more significant returns over longer periods.
  

3. Applications:
   

• Simple Interest: Ideal for short-term loans and investments.
  
• Compound Interest: Best suited for long-term investments and savings, where reinvestment can maximise returns.
  

Excel Example: Calculating Simple and Compound Interest

Excel offers straightforward formulas to calculate both simple and compound interest, making it a practical tool for financial planning.

Simple Interest Calculation in Excel:

To calculate simple interest, use the formula:
=Principal * Rate * Time

For example, if you invest ₹1,000 at a 5% interest rate for 3 years:
Excel
Copy code
=1000 * 0.05 * 3

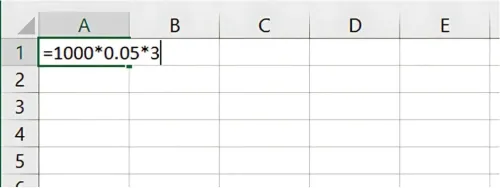
Result: 150

Compound Interest Calculation in Excel:

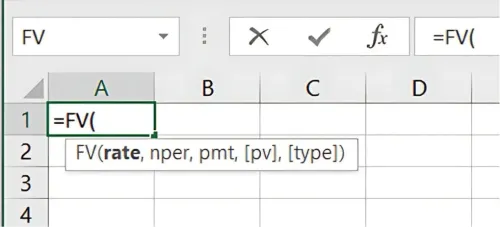
For compound interest, you can use the FV function:

=FV(rate, nper, pmt, [pv], [type])

To calculate the future value of a ₹1,000 investment at a 5% interest rate for 3 years:

=FV(0.05, 3, 0, -1000)

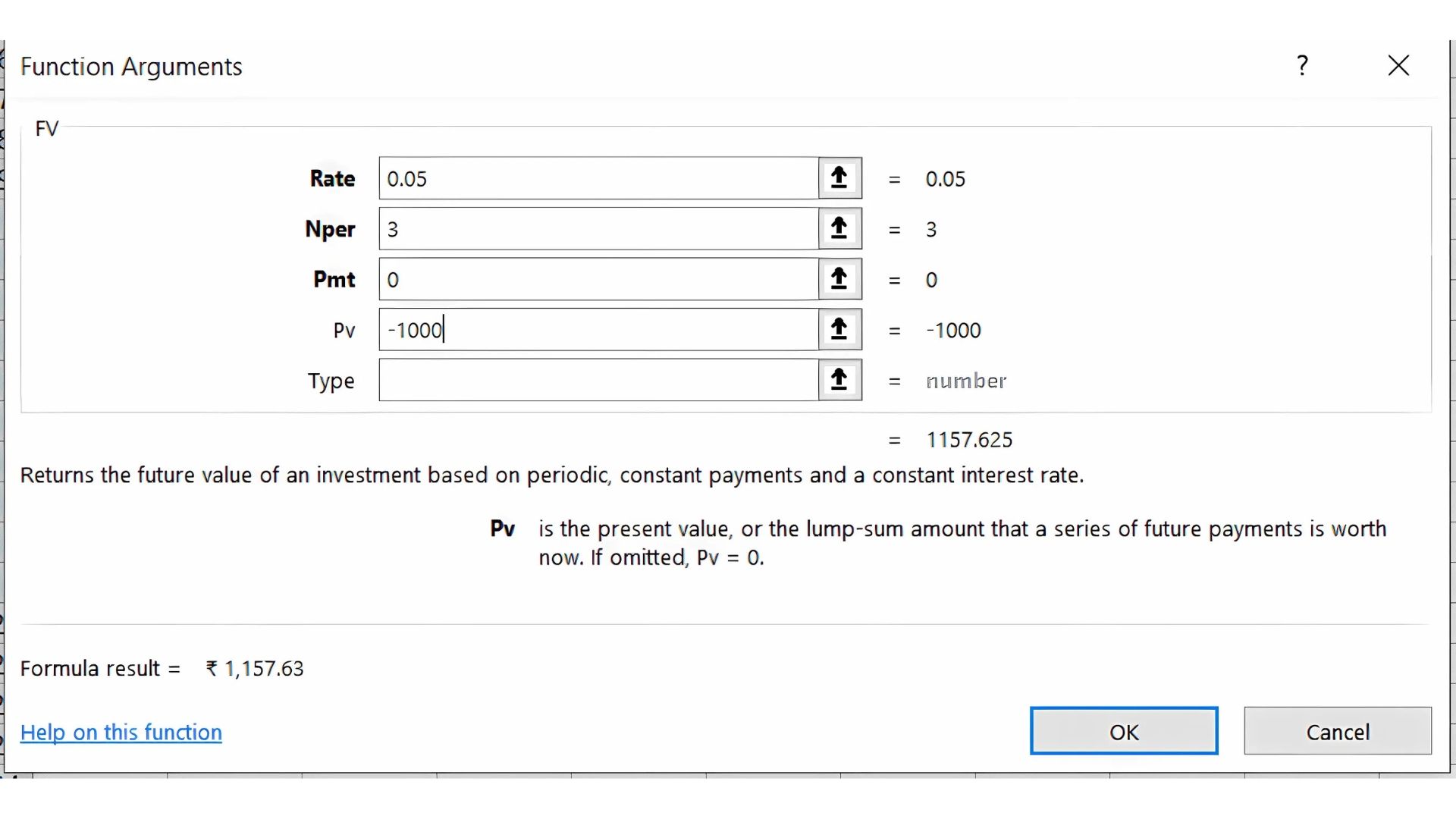
Result: 1157.63

Real-World Applications

• Simple Interest is commonly used for personal loans, auto loans, and short-term investments where the growth rate is predictable.
• Compound Interest is prevalent in savings accounts, retirement funds, and other investments where reinvestment boosts returns over time.

Key Takeaways:

• Simple Interest is straightforward and ideal for short-term financial commitments.
• Compound Interest can significantly enhance returns over the long term due to the "interest on interest" effect.
• Using Excel functions like FV helps automate these calculations, making financial analysis easier.

Conclusion:

Knowing the differences between simple and compound interest is essential for effective financial planning. Whether you are an investor seeking maximum returns or a borrower aiming to manage loan costs, understanding these concepts can guide you in making better decisions.

Next Chapter Preview: In the next chapter, we’ll explore How to Calculate Loan Amortisation Schedules Using Excel, which will provide step-by-step instructions for building a schedule that breaks down each payment into principal and interest. Stay tuned to master this essential tool for managing loans!