Compound Interest Calculation: Step-by-Step in Excel

Compound interest is often referred to as "interest on interest." Unlike simple interest, where interest is calculated only on the principal amount, compound interest considers both the initial principal and the accumulated interest over previous periods. This makes it a powerful tool in finance, especially when projecting the growth of investments or loans.

In this blog, we'll break down compound interest and explain how to calculate it step-by-step in Excel, using simple formulas and examples to show how your money can grow exponentially over time.

What is Compound Interest?

Compound interest refers to the process where the interest earned or paid on a principal is reinvested, causing the interest to generate more interest over time. It contrasts with simple interest, which is calculated solely on the principal amount.

Key Components of Compound Interest:

1. Principal (P): The original sum of money invested or borrowed.
2. Interest Rate (r): The annual rate at which interest is applied.
3. Time Period (n): The number of compounding periods, typically in years.
4. Compounding Frequency: The number of times the interest is compounded per period (e.g., annually, quarterly, monthly, daily).

Formula for Compound Interest:

A = P × (1 + r/n)^nt

Where:

• A = Amount (Future Value)
• P = Principal
• r = Annual interest rate (in decimal form)
• n = Number of times interest is compounded per year
• t = Time (years)

Example of Compound Interest Calculation

Suppose you invest ₹1,000 for 3 years at an annual interest rate of 5%, compounded annually.

Step-by-Step Calculation:

1. Principal (P) = ₹1,000
2. Annual Interest Rate (r) = 5% or 0.05
3. Time (t) = 3 years
4. Compounding Frequency (n) = 1 (compounded annually)

Using the compound interest formula:

A = 1000 × (1 + 0.05/1)^(1×3) = 1000 × 1.157625 = 1157.63

After 3 years, the total amount would be ₹1,157.63.

Compound Interest Calculation in Excel

Excel simplifies the process of calculating compound interest. You can use the FV function, which stands for Future Value, to compute how much an investment will grow with compound interest.

Step-by-Step Excel Example: Use the FV formula in Excel: The syntax is:

=FV(rate, nper, pmt, [pv], [type])

• Rate: The interest rate per period (annual interest rate).
• nper: The total number of periods (years).
• pmt: Payment made in each period (0 if there is no periodic payment).
• pv: Present value (the initial investment).
• type: When payments are due (optional, can be left blank or set to 0).

Example in Excel: Suppose you invest ₹1,000 at a 5% annual interest rate for 3 years, compounded annually. You can calculate it as follows: Excel Copy code =FV(0.05, 3, 0, -1000)

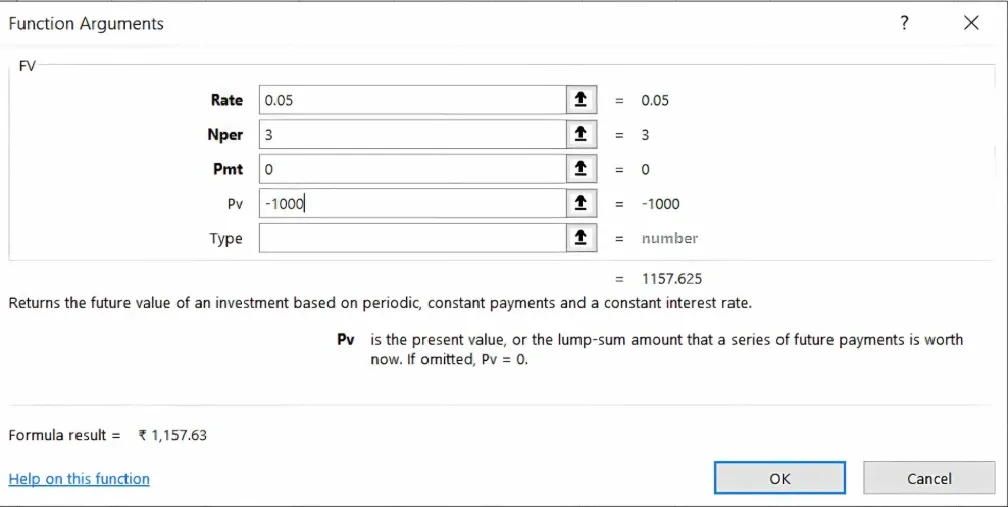
Result: 1157.63

Advantages of Compound Interest:

1. Exponential Growth: Compound interest allows money to grow faster over time because it includes both the principal and accumulated interest in the calculations.

2. Long-Term Benefits: The longer you leave money invested, the greater the impact of compound interest. This is why starting to invest early is crucial for long-term financial growth.

3. Multiple Compounding Frequencies: The frequency of compounding (annually, quarterly, monthly) can significantly affect the total interest earned. More frequent compounding periods result in higher overall returns.

Excel Formula for Different Compounding Periods

To calculate compound interest with different compounding frequencies, you can modify the formula in Excel accordingly.

• Annual Compounding: =FV(rate, nper, 0, -pv)

Quarterly Compounding: Divide the annual interest rate by 4 and multiply the number of periods by 4: Excel Copy code =FV(0.05/4, 3*4, 0, -1000)

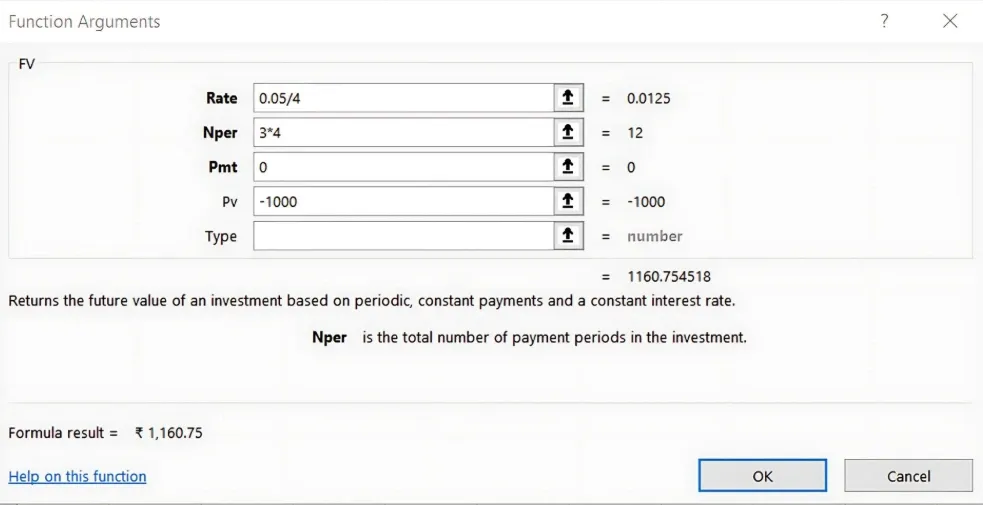
Result: 1160.75

Monthly Compounding: Divide the annual interest rate by 12 and multiply the number of periods by 12: Excel Copy code =FV(0.05/12, 3*12, 0, -1000)

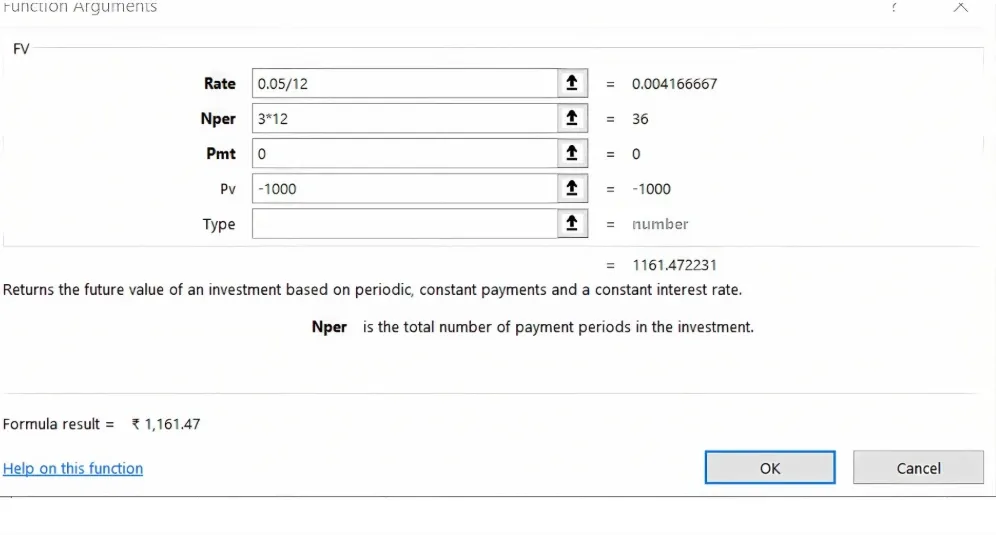
Result: 1161.47

Real-World Applications of Compound Interest

Compound interest plays a critical role in various financial scenarios:

• Savings Accounts: Many savings accounts offer compound interest, allowing your money to grow faster over time.

• Investments: Long-term investments in stocks or bonds benefit greatly from compound interest, especially with frequent compounding.

• Loans: Loans like mortgages and student loans often use compound interest, which increases the total amount to be repaid.

Key Takeaways:

• Compound interest is a powerful financial tool that grows your money faster by reinvesting interest.
• The more frequently the interest is compounded, the higher the total returns.
• Excel offers simple formulas like FV to quickly calculate compound interest, making financial planning easier.

Conclusion:

Compound interest can significantly boost your wealth over time. Mastering compound interest calculations, especially using Excel, is a valuable skill for investors, savers, and financial professionals alike.

Next Chapter Preview: In the next chapter, we will explore Simple Interest vs. Compound Interest—breaking down their key differences and learning their respective calculation techniques. Stay tuned to see how these two approaches impact financial growth!