IRR and XIRR Functions: Calculating Returns with Variable Cash Flows

In financial analysis, calculating the return on investment with regular or irregular cash flows is essential for evaluating the profitability of projects or investments. The Internal Rate of Return (IRR) and Extended Internal Rate of Return (XIRR) functions in Excel are powerful tools that help assess the returns based on both consistent and variable cash flows.

This blog will guide you through using IRR and XIRR functions to calculate the return on investment, with examples that illustrate how these functions work in different scenarios.

What is IRR?

Internal Rate of Return (IRR) is the discount rate at which the Net Present Value (NPV) of all cash flows (both positive and negative) from an investment equals zero. It represents the breakeven point where the value of future cash inflows balances out the initial investment.

The formula for IRR:
0 = ∑ [Cₜ / (1 + IRR)^t]
from t = 1 to n

Where:

Cₜ = Cash flow at time t
n = Number of periods (years)
IRR =Internal Rate of Return

Step-by-Step Guide: Using the IRR Function in Excel

Example:

You invest ₹10,000 today, and the project generates the following cash flows over 4 years:

To calculate the IRR in Excel:
1 .Set Up the Data: List the cash flows in a column.

Use the IRR Formula:
=IRR(B1:B5)

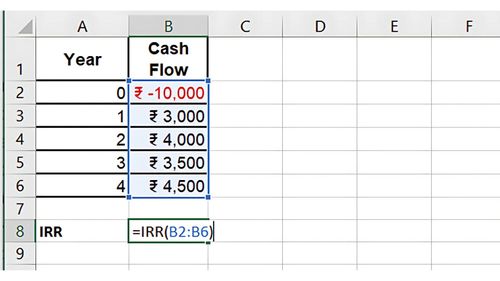
2. Result: The IRR for this investment might be around 12%, meaning this is the rate of return where the NPV equals zero. What is XIRR?

Extended Internal Rate of Return (XIRR) is an extension of the IRR function that handles irregular cash flows occurring at specific dates. XIRR is ideal for situations where cash flows are not evenly spaced over time, such as investment projects with variable payments or receipts.

The formula for XIRR:
0 = ∑ [Cₜ / (1 + XIRR)^((dₜ - d₀) / 365)]
from t = 1 to n

Where:

• Cₜ = Cash flow at time t
  

• dₜ = Date of cash flow t
  

• d₀ = Date of initial investment
  

• XIRR = Extended Internal Rate of Return
  

Step-by-Step Guide: Using the XIRR Function in Excel

Example:

Consider the same investment of ₹10,000, but the cash flows occur on irregular dates:

1. Set Up the Data: In one column, list the dates of the cash flows, and in another, list the cash flow amounts.

Use the XIRR Formula:

=XIRR(B1:B5, A1:A5)

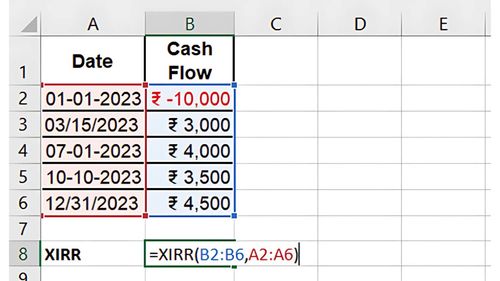
2. Result: XIRR provides a return based on the specific timing of each cash flow, likely higher than the IRR due to the irregular cash flow dates.

Benefits of Using IRR and XIRR

• IRR helps evaluate the profitability of projects or investments with regular cash flows.
  

• XIRR handles cash flows that are unevenly spaced over time, making it useful for real-world projects with variable payments or receipts.
  

• Both functions provide valuable insights into whether a project meets or exceeds the required rate of return.
  

Key Takeaways:

• The IRR function calculates the return on investment with regular cash flows.
  

• The XIRR function accounts for irregular cash flows, providing a more precise return calculation when dates vary.
  

• Both functions are crucial for evaluating investment performance in real-world scenarios.
  

Conclusion:

Understanding and using the IRR and XIRR functions in Excel allows you to assess the return on investments, even when cash flows are variable. These calculations are essential for making informed financial decisions, especially when comparing different investment options or projects.

Next Chapter Preview: In the next chapter, we will explore the PMT, RATE, NPER, CUMIPMT, and CUMPRINC functions for Loan-related Calculations, showing how these functions can help manage and calculate different aspects of loans, including monthly payments, interest, and principal. Stay tuned for more insights on loan management in Excel!