Kotak
Stockshaala
Chapter 3 | 3 min read
सिंपल इंटरेस्ट (simple interest) बनाम कंपाउंड इंटरेस्ट (compound interest): कैलकुलेशन टेक्निक्स (calculation techniques)
वित्त में साधारण ब्याज और कंपाउंड इंटरेस्ट (compound interest) के बीच के अंतर को समझना बहुत महत्वपूर्ण है, क्योंकि यह आपको इन्वेस्टमेंट्स (investments), लोन (loans), और सेविंग्स (savings) के बारे में सूचित निर्णय लेने में मदद करता है। दोनों में ब्याज का भुगतान या अर्जन शामिल होता है, लेकिन उनकी गणना विधियाँ आपके निवेश की वृद्धि या लोन की कुल लागत पर महत्वपूर्ण प्रभाव डालती हैं। इस ब्लॉग में, हम प्रत्येक के लिए गणना तकनीकों का पता लगाएंगे और उन्हें प्रभावी ढंग से उपयोग करने के तरीके को समझाएंगे।
साधारण ब्याज क्या है? (What is Simple Interest?)
साधारण ब्याज एक तरीका है जिसमें ब्याज केवल प्रारंभिक राशि या प्रिंसिपल (principal) पर पूरी अवधि के लिए लगाया जाता है। यह कंपाउंडिंग (compounding) के प्रभाव को नहीं मानता, जिससे यह सरल और पूर्वानुमेय हो जाता है।
साधारण ब्याज का फार्मूला:
SI = P × r × t
जहां:
- SI = साधारण ब्याज
- P = प्रिंसिपल (प्रारंभिक निवेश या लोन की राशि)
- r = प्रति अवधि ब्याज दर (दशमलव के रूप में व्यक्त)
- t = समय (वर्षों में)
उदाहरण:
यदि आप ₹1,000 को 5% ब्याज दर पर 3 वर्षों के लिए निवेश करते हैं, तो साधारण ब्याज की गणना होगी:
SI = 1000 × 0.05 × 3 = 150
तो, 3 वर्षों में अर्जित ब्याज ₹150 होगा, जिससे कुल राशि ₹1,150 हो जाएगी।
कंपाउंड इंटरेस्ट क्या है? (What is Compound Interest?)
कंपाउंड इंटरेस्ट (compound interest) साधारण ब्याज के विचार को आगे बढ़ाता है, जिसमें ब्याज को प्रिंसिपल और पहले से संचित ब्याज में जोड़ा जाता है। इसका मतलब है कि आप "ब्याज पर ब्याज" अर्जित करते हैं, जिससे समय के साथ एक्सपोनेंशियल (exponential) वृद्धि होती है।
कंपाउंड इंटरेस्ट का फार्मूला:
A = P × (1 + r/n)^(n × t)
जहां:
- A = राशि (भविष्य का मूल्य)
- P = प्रिंसिपल (प्रारंभिक निवेश या लोन की राशि)
- r = वार्षिक ब्याज दर (दशमलव के रूप में)
- n = प्रति वर्ष ब्याज कंपाउंड होने की संख्या
- t = समय (वर्षों में)
उदाहरण:
यदि आप ₹1,000 को 5% वार्षिक ब्याज दर पर 3 वर्षों के लिए निवेश करते हैं, वार्षिक रूप से कंपाउंड:
A = 1000 × (1 + 0.05/1)^(1 × 3) = 1000 × (1.05)^3 = 1157.63
कुल राशि ₹1,157.63 होगी, जिसमें अर्जित ब्याज ₹157.63 है।
साधारण और कंपाउंड इंटरेस्ट के बीच मुख्य अंतर (Key Differences Between Simple and Compound Interest)
- ब्याज गणना (Interest Calculation):
- साधारण ब्याज: ब्याज केवल प्रिंसिपल पर गणना की जाती है।
- कंपाउंड इंटरेस्ट: ब्याज प्रिंसिपल और संचित ब्याज दोनों पर गणना की जाती है।
- वृद्धि पैटर्न (Growth Pattern):
- साधारण ब्याज: रैखिक रूप से बढ़ता है; अर्जित ब्याज प्रत्येक अवधि में समान रहता है।
- कंपाउंड इंटरेस्ट: एक्सपोनेंशियली (exponentially) बढ़ता है, लंबे समय तक अधिक महत्वपूर्ण रिटर्न के साथ।
- आवेदन (Applications):
- साधारण ब्याज: अल्पकालिक लोन और निवेश के लिए आदर्श।
- कंपाउंड इंटरेस्ट: लंबी अवधि के निवेश और बचत के लिए सबसे उपयुक्त है, जहां पुनर्निवेश रिटर्न को अधिकतम कर सकता है।
एक्सेल उदाहरण: साधारण और कंपाउंड इंटरेस्ट की गणना (Excel Example: Calculating Simple and Compound Interest)
एक्सेल सरल फार्मूलों के साथ साधारण और कंपाउंड इंटरेस्ट की गणना करने की सुविधा प्रदान करता है, जिससे यह वित्तीय योजना के लिए एक व्यावहारिक उपकरण बन जाता है।
एक्सेल में साधारण ब्याज की गणना:
साधारण ब्याज की गणना करने के लिए, फार्मूला का उपयोग करें:
=Principal * Rate * Time
उदाहरण के लिए, यदि आप ₹1,000 को 5% ब्याज दर पर 3 वर्षों के लिए निवेश करते हैं:
Excel
Copy code
=1000 * 0.05 * 3
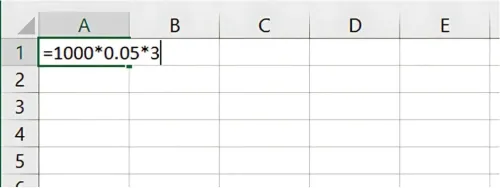
परिणाम (Result): 150
कंपाउंड इंटरेस्ट (compound interest) की गणना एक्सेल (Excel) में:
कंपाउंड इंटरेस्ट (compound interest) के लिए, आप FV फंक्शन (function) का उपयोग कर सकते हैं:
=FV(rate, nper, pmt, [pv], [type])
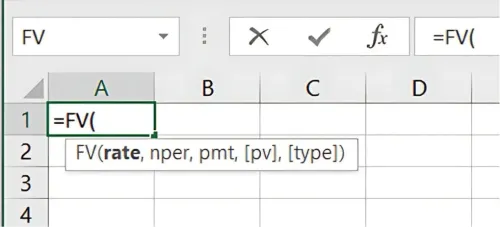
₹1,000 के इन्वेस्टमेंट (investment) का भविष्य मूल्य 5% इंटरेस्ट रेट (interest rate) पर 3 वर्षों के लिए कैलकुलेट (calculate) करने के लिए:
=FV(0.05, 3, 0, -1000)
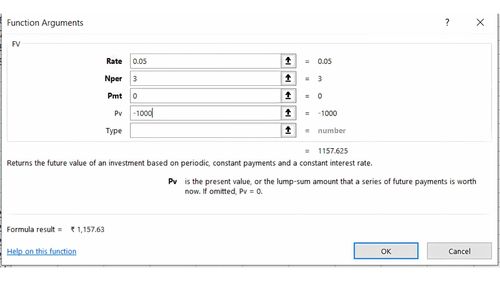
Result: 1157.63
रियल-वर्ल्ड एप्लिकेशन्स (Real-World Applications)
- सिंपल इंटरेस्ट (simple interest) का उपयोग आमतौर पर पर्सनल लोन (personal loans), ऑटो लोन (auto loans), और शॉर्ट-टर्म इन्वेस्टमेंट्स (short-term investments) में किया जाता है जहाँ ग्रोथ रेट (growth rate) प्रेडिक्टेबल (predictable) होता है।
- कंपाउंड इंटरेस्ट (compound interest) सेविंग्स अकाउंट्स (savings accounts), रिटायरमेंट फंड्स (retirement funds), और अन्य इन्वेस्टमेंट्स (investments) में प्रचलित है जहाँ री-इन्वेस्टमेंट (reinvestment) समय के साथ रिटर्न्स (returns) को बढ़ाता है।
की टेकअवे (Key Takeaways):
- सिंपल इंटरेस्ट (simple interest) सीधा है और शॉर्ट-टर्म फाइनेंशियल कमिटमेंट्स (short-term financial commitments) के लिए आदर्श है।
- कंपाउंड इंटरेस्ट (compound interest) लंबे समय में रिटर्न्स (returns) को काफी बढ़ा सकता है "इंटरेस्ट ऑन इंटरेस्ट (interest on interest)" इफ़ेक्ट के कारण।
- एक्सेल (Excel) फंक्शन्स जैसे FV इन कैलकुलेशन्स (calculations) को ऑटोमेट करने में मदद करता है, जिससे फाइनेंशियल एनालिसिस (financial analysis) आसान हो जाता है।
निष्कर्ष (Conclusion):
सिंपल और कंपाउंड इंटरेस्ट के बीच के अंतर को जानना प्रभावी फाइनेंशियल प्लानिंग (financial planning) के लिए आवश्यक है। चाहे आप एक इन्वेस्टर (investor) हों जो अधिकतम रिटर्न्स (returns) की तलाश में है या एक बोर्रोअर (borrower) जो लोन कॉस्ट्स (loan costs) को मैनेज करना चाहता है, इन कॉन्सेप्ट्स (concepts) को समझना बेहतर निर्णय लेने में आपकी मदद कर सकता है।
अगला अध्याय पूर्वावलोकन (Next Chapter Preview): अगले अध्याय में, हम कैसे एक्सेल (Excel) का उपयोग करके लोन एमोर्टाइजेशन शेड्यूल्स (loan amortisation schedules) की गणना करें, एक्सप्लोर करेंगे, जो प्रत्येक भुगतान को प्रिंसिपल (principal) और इंटरेस्ट (interest) में डिवाइड करने के लिए स्टेप-बाय-स्टेप इंस्ट्रक्शन्स (step-by-step instructions) प्रदान करेगा। इस आवश्यक टूल (essential tool) को मास्टर करने के लिए जुड़े रहें!
This content has been translated using a translation tool. We strive for accuracy; however, the translation may not fully capture the nuances or context of the original text. If there are discrepancies or errors, they are unintended, and we recommend original language content for accuracy.
Disclaimer: This article is for informational purposes only and does not constitute financial advice. It is not produced by the desk of the Kotak Neo Research Team, nor is it a report published by the Kotak Neo Research Team. The information presented is compiled from several secondary sources available on the internet and may change over time. Investors should conduct their own research and consult with financial professionals before making any investment decisions. Read the full disclaimer here.
Investments in securities market are subject to market risks, read all the related documents carefully before investing. Brokerage will not exceed SEBI prescribed limit. The securities are quoted as an example and not as a recommendation. SEBI Registration No-INZ000200137 Member Id NSE-08081; BSE-673; MSE-1024, MCX-56285, NCDEX-1262.
Recommended Courses for you
Learn, Invest, and Grow with Kotak Videos
Explore our comprehensive video library that blends expert market insights with Kotak's innovative financial solutions to support your goals.
Trading with collateral as margin with Kotak Neo
How India is Redefining Space Exploration
