

Kotak
Stockshaala
Chapter 2 | 5 min read
कंपाउंड इंटरेस्ट (compound interest) कैलकुलेशन: स्टेप-बाय-स्टेप (step-by-step) इन एक्सेल (Excel)
कंपाउंड इंटरेस्ट (compound interest) को अक्सर "इंटरेस्ट ऑन इंटरेस्ट" के रूप में जाना जाता है। साधारण ब्याज की तुलना में, जहां ब्याज केवल मूलधन पर गणना की जाती है, कंपाउंड इंटरेस्ट (compound interest) प्रारंभिक मूलधन और पूर्व अवधि के संचित ब्याज दोनों पर विचार करता है। यह वित्त में एक शक्तिशाली उपकरण बनाता है, विशेष रूप से निवेश या ऋण के विकास को प्रोजेक्ट करते समय।
इस ब्लॉग में, हम कंपाउंड इंटरेस्ट (compound interest) को सरलता से समझाएंगे और एक्सेल (Excel) में इसे स्टेप-बाय-स्टेप कैसे कैलकुलेट किया जाए, इस पर चर्चा करेंगे, जिससे यह दिखाया जा सके कि आपका पैसा समय के साथ एक्सपोनेंशियली (exponentially) कैसे बढ़ सकता है।
कंपाउंड इंटरेस्ट (Compound Interest) क्या है?
कंपाउंड इंटरेस्ट (compound interest) उस प्रक्रिया को संदर्भित करता है जहां किसी मूलधन पर अर्जित या भुगतान किया गया ब्याज पुनर्निवेशित किया जाता है, जिससे ब्याज समय के साथ अधिक ब्याज उत्पन्न करता है। यह साधारण ब्याज के विपरीत है, जो केवल मूलधन पर गणना की जाती है।
कंपाउंड इंटरेस्ट (Compound Interest) के प्रमुख घटक:
- प्रिंसिपल (Principal) (P): निवेश या उधार ली गई मूल राशि।
- इंटरेस्ट रेट (Interest Rate) (r): वह वार्षिक दर जिस पर ब्याज लागू होता है।
- टाइम पीरियड (Time Period) (n): कंपाउंडिंग अवधियों की संख्या, आमतौर पर वर्षों में।
- कंपाउंडिंग फ्रीक्वेंसी (Compounding Frequency): प्रति अवधि जितनी बार ब्याज कंपाउंड किया जाता है (जैसे, वार्षिक, त्रैमासिक, मासिक, दैनिक)।
कंपाउंड इंटरेस्ट (Compound Interest) का फॉर्मूला:
A = P × (1 + r/n)^nt
जहां:
- A = राशि (भविष्य मूल्य)
- P = प्रिंसिपल (Principal)
- r = वार्षिक इंटरेस्ट रेट (annual interest rate) (दशमलव रूप में)
- n = प्रति वर्ष ब्याज कंपाउंडिंग की संख्या
- t = समय (वर्षों में)
कंपाउंड इंटरेस्ट (Compound Interest) कैलकुलेशन का उदाहरण
मान लीजिए आप ₹1,000 का निवेश 3 वर्षों के लिए 5% वार्षिक ब्याज दर पर करते हैं, जो वार्षिक रूप से कंपाउंड होता है।
स्टेप-बाय-स्टेप कैलकुलेशन:
- प्रिंसिपल (P) = ₹1,000
- वार्षिक इंटरेस्ट रेट (r) = 5% या 0.05
- समय (t) = 3 वर्ष
- कंपाउंडिंग फ्रीक्वेंसी (n) = 1 (वार्षिक रूप से कंपाउंड)
कंपाउंड इंटरेस्ट (compound interest) फॉर्मूला का उपयोग करते हुए:
A = 1000 × (1 + 0.05/1)^(1×3) = 1000 × 1.157625 = 1157.63
3 वर्षों के बाद, कुल राशि ₹1,157.63 होगी।
एक्सेल (Excel) में कंपाउंड इंटरेस्ट (Compound Interest) कैलकुलेशन
एक्सेल (Excel) कंपाउंड इंटरेस्ट (compound interest) की गणना की प्रक्रिया को सरल बनाता है। आप FV फंक्शन (FV function) का उपयोग कर सकते हैं, जो फ्यूचर वैल्यू (Future Value) के लिए है, यह गणना करने के लिए कि कंपाउंड इंटरेस्ट (compound interest) के साथ निवेश कितना बढ़ेगा।
स्टेप-बाय-स्टेप एक्सेल (Excel) उदाहरण: एक्सेल (Excel) में FV फॉर्मूला का उपयोग करें: सिंटैक्स है:
=FV(rate, nper, pmt, [pv], [type])
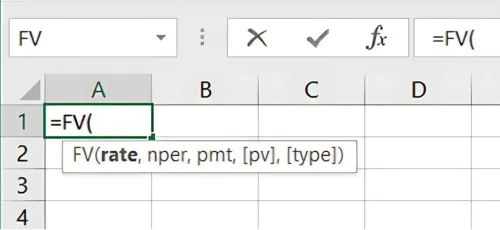
- रेट (rate): प्रति अवधि का इंटरेस्ट रेट (interest rate) (वार्षिक इंटरेस्ट रेट (annual interest rate))।
- एनपर (nper): कुल अवधि की संख्या (वर्षों में)।
- पीएमटी (pmt): हर अवधि में किया गया भुगतान (यदि कोई नियमित भुगतान नहीं है तो 0)।
- पीवी (pv): प्रेजेंट वैल्यू (present value) (प्रारंभिक निवेश)।
- टाइप (type): भुगतान कब होते हैं (वैकल्पिक, इसे खाली छोड़ा जा सकता है या 0 पर सेट किया जा सकता है)।
Excel में उदाहरण: मान लीजिए आप ₹1,000 को 5% वार्षिक इंटरेस्ट रेट (annual interest rate) पर 3 वर्षों के लिए इन्वेस्ट करते हैं, और यह वार्षिक कंपाउंड होता है। आप इसे इस प्रकार कैलकुलेट कर सकते हैं: Excel Copy code =FV(0.05, 3, 0, -1000)
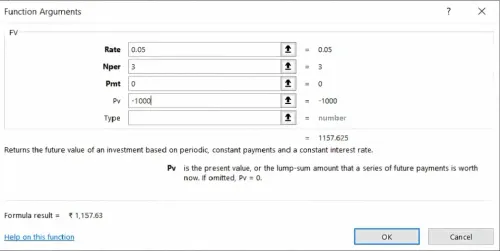
नतीजा: 1157.63
कंपाउंड इंटरेस्ट (compound interest) के फायदे:
-
एक्सपोनेंशियल ग्रोथ (exponential growth): कंपाउंड इंटरेस्ट (compound interest) पैसे को तेजी से बढ़ने की सुविधा देता है क्योंकि इसमें प्रिंसिपल और संचित ब्याज दोनों शामिल होते हैं।
-
लॉन्ग-टर्म बेनिफिट्स (long-term benefits): जितना लंबे समय तक आप पैसे को इन्वेस्टेड (invested) रखते हैं, कंपाउंड इंटरेस्ट (compound interest) का प्रभाव उतना ही अधिक होता है। यही कारण है कि जल्दी इन्वेस्ट (invest) करना लम्बे समय के वित्तीय विकास के लिए महत्वपूर्ण है।
-
मल्टीपल कंपाउंडिंग फ्रीक्वेंसीज (multiple compounding frequencies): कंपाउंडिंग (compounding) की फ्रीक्वेंसी (frequency) (एन्युअली, क्वार्टरली, मंथली) कुल कमाए गए ब्याज को काफी प्रभावित कर सकती है। अधिक बार कंपाउंडिंग (compounding) पीरियड्स (periods) के परिणामस्वरूप उच्च कुल रिटर्न्स (returns) मिलते हैं।
अलग-अलग कंपाउंडिंग पीरियड्स (compounding periods) के लिए एक्सेल फॉर्मूला (Excel formula)
विभिन्न कंपाउंडिंग फ्रीक्वेंसीज (compounding frequencies) के साथ कंपाउंड इंटरेस्ट (compound interest) की गणना करने के लिए, आप एक्सेल (Excel) में फॉर्मूला को उसी अनुसार संशोधित कर सकते हैं।
- एन्युअल कंपाउंडिंग (annual compounding): =FV(rate, nper, 0, -pv)
क्वार्टरली कंपाउंडिंग (quarterly compounding): एन्युअल इंटरेस्ट रेट (annual interest rate) को 4 से विभाजित करें और पीरियड्स (periods) की संख्या को 4 से गुणा करें: Excel Copy code =FV(0.05/4, 3*4, 0, -1000)

रिजल्ट (Result): 1160.75
मंथली कंपाउंडिंग (Monthly Compounding): एनुअल इंटरेस्ट रेट (annual interest rate) को 12 से डिवाइड करें और पीरियड्स (periods) की संख्या को 12 से मल्टिप्लाई करें: Excel Copy code =FV(0.05/12, 3*12, 0, -1000)
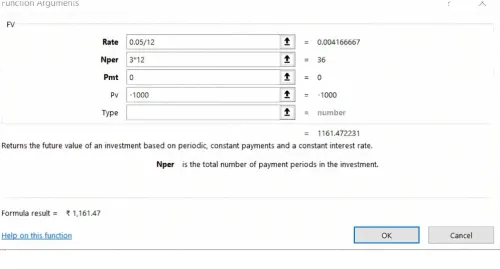
Result: 1161.47
कंपाउंड इंटरेस्ट (compound interest) के वास्तविक जीवन में उपयोग
कंपाउंड इंटरेस्ट (compound interest) विभिन्न वित्तीय परिस्थितियों में महत्वपूर्ण भूमिका निभाता है:
-
सेविंग्स अकाउंट्स (savings accounts): कई सेविंग्स अकाउंट्स (savings accounts) कंपाउंड इंटरेस्ट (compound interest) ऑफर करते हैं, जिससे आपका पैसा समय के साथ तेजी से बढ़ता है।
-
इन्वेस्टमेंट्स (investments): लॉन्ग-टर्म इन्वेस्टमेंट्स (long-term investments) स्टॉक्स (stocks) या बॉन्ड्स (bonds) में कंपाउंड इंटरेस्ट (compound interest) से काफी लाभ उठाते हैं, खासकर जब फ्रीक्वेंट कंपाउंडिंग (frequent compounding) होती है।
-
लोन (loans): मॉर्टगेज (mortgages) और स्टूडेंट लोन (student loans) जैसे लोन (loans) अक्सर कंपाउंड इंटरेस्ट (compound interest) का उपयोग करते हैं, जिससे चुकाने की कुल राशि बढ़ जाती है।
मुख्य बिंदु (Key Takeaways):
- कंपाउंड इंटरेस्ट (compound interest) एक शक्तिशाली वित्तीय टूल (financial tool) है जो आपके पैसे को तेजी से बढ़ाता है बाय (by) रिइन्वेस्टिंग (reinvesting) इंटरेस्ट (interest)।
- जितनी बार इंटरेस्ट (interest) कंपाउंड (compound) होता है, उतने ही अधिक कुल रिटर्न्स (total returns) होते हैं।
- एक्सेल (Excel) सरल फार्मूले जैसे एफवी (FV) ऑफर करता है तेजी से कंपाउंड इंटरेस्ट (compound interest) कैलकुलेट (calculate) करने के लिए, जिससे वित्तीय योजना बनाना आसान हो जाता है।
निष्कर्ष (Conclusion):
कंपाउंड इंटरेस्ट (compound interest) समय के साथ आपकी वेल्थ (wealth) को महत्वपूर्ण रूप से बढ़ा सकता है। कंपाउंड इंटरेस्ट (compound interest) कैलकुलेशन (calculation) में महारत हासिल करना, विशेष रूप से एक्सेल (Excel) का उपयोग करके, निवेशकों, सेवर्स (savers), और वित्तीय पेशेवरों (financial professionals) के लिए एक मूल्यवान स्किल (valuable skill) है।
अगले अध्याय का पूर्वावलोकन (Next Chapter Preview): अगले अध्याय में, हम सिंपल इंटरेस्ट (simple interest) बनाम कंपाउंड इंटरेस्ट (compound interest) की खोज करेंगे—उनके प्रमुख अंतर को तोड़कर और उनके संबंधित कैलकुलेशन (calculation) तकनीकों को सीखेंगे। देखते रहिए कि ये दो दृष्टिकोण वित्तीय वृद्धि को कैसे प्रभावित करते हैं!
This content has been translated using a translation tool. We strive for accuracy; however, the translation may not fully capture the nuances or context of the original text. If there are discrepancies or errors, they are unintended, and we recommend original language content for accuracy.
Recommended Courses for you
Beyond Stockshaala
Discover our extensive knowledge center
Learn, Invest, and Grow with Kotak Videos
Explore our comprehensive video library that blends expert market insights with Kotak's innovative financial solutions to support your goals.














